OEF 同余算术
--- 介绍 ---
本模块目前包含 37 个有限环  /n
/n 里的计算的练习.
里的计算的练习.
加法填空
考虑映射
, 它把
映到
. 根据
的值把底下方块里的数拖放到空格里去.
同余类
?
带参数同余
计算
模 , 写成
的函数,
是 0 到 9 之间的一个数字. 约定 : 回答中的出现的整数应该在 0 和 之间.
立方填空
考虑映射
, 它把
映到
. 根据
的值把底下方块里的数拖放到空格里去.
除法填空
考虑映射
, 它把
映到
. 根据
的值把底下方块里的数拖放到空格里去.
除法 I
在  /
/ 里计算 / . 把结果表示成 0 到 的整数.
里计算 / . 把结果表示成 0 到 的整数.
除法 II
在  /
/ 里计算 / . 把结果表示成 0 到 的整数.
里计算 / . 把结果表示成 0 到 的整数.
除法 III
在  /
/ 里计算 / . 把结果表示成 0 到 的整数.
里计算 / . 把结果表示成 0 到 的整数.
零因子
是  /
/ 里的零因子吗 ?
里的零因子吗 ?
零因子 II
找出  /
/ 里的零因子集. (这个练习的零因子不包括 0.)
里的零因子集. (这个练习的零因子不包括 0.) 把每个元素写成 1 到 之间的一个整数, 元素间用逗号分隔.
零因子 III
已知 =2, 其中 是素数. 在  /
/ 里有多少零因子 ?
里有多少零因子 ? 本练习中的零因子不包括 0.
模 p^2 的根
设多项式
在  /
/ 内有两个根
与
.
计算之.
内有两个根
与
.
计算之.
(写成 0 到 之间的整数的形式).
设在  内
.
计算
mod
.
内
.
计算
mod
.
(出现的整数应该在 0 到
) 之间.
你找到了
mod
.
因此, 方程
mod
等价于
mod
.
是否存在唯一的 0 与
之间的整数
同余于 mod 且使得
mod
?
回答 :
方程
mod
实际上等价于方程
mod . 计算 0 与
之间的整数
, 它同余于 mod 且使得
mod
.
方程
mod
有多少解 (模
) 它同余于 mod ?
求逆 I
在  /
/ 里求 的逆 . 把结果表示成 0 到 间的整数.
里求 的逆 . 把结果表示成 0 到 间的整数.
求逆 II
在  /
/ 里求 的逆 . 把结果表示成 0 到 的整数.
里求 的逆 . 把结果表示成 0 到 的整数.
求逆 III
在  /
/ 里求 的逆 . 把结果表示成 0 到 的整数.
里求 的逆 . 把结果表示成 0 到 的整数.
可逆乘幂
是素数. 考虑函数 f:  /
/ ->
->  /
/ 它定义为 f(x)=x .
它定义为 f(x)=x . f 是双射吗 ?
可除性
假定对两个整数
和
, 素数 整除
. 是否有 整除
和
?
同余线性方程
设有  内方程
内方程
 mod
mod
方程有解吗 ?
解的集合
具有形式
 其中
是正整数,
是
其中
是正整数,
是 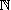 内严格小于
的整数的有限集. 取
为其中最小者, 给出
内所有整数 .
解的集合
具有形式
内严格小于
的整数的有限集. 取
为其中最小者, 给出
内所有整数 .
解的集合
具有形式
 其中
是
内严格小于 的整数的有限集. 写出
的所有整数.
其中
是
内严格小于 的整数的有限集. 写出
的所有整数.
+


把常数项 换成另一个整数使得新方程有解.
乘法填空
考虑映射
, 它把
映到
. 根据
的值把底下方块里的数拖放到空格里去.
特殊倍数
设
. 求最小的整数
使得写成
进制数时变成
个 1 的整数也是
的倍数 .
特殊倍数 II
设
. 这是一个素数. 求最小整数
, 使得一个整数写成
进数时具有形式
其中有
个重复片断 , 这个数也是
的倍数.
以 b 为底的有理数的周期
有理数
写成 进制小数时以 为周期循环, 而且是从第 位小数开始循环. 问
的分母可能有的素因子是什么 (写成十进制形式) ?
多项式填空
考虑映射
, 它把
映到
. 根据
的值把底下方块里的数拖放到空格里去.
乘幂
在  /
/ 内计算 . 把结果表示成 0 到 间的整数.
内计算 . 把结果表示成 0 到 间的整数.
乘幂 II
是素数. 在  /
/ 内计算 . 把结果表示成 0 到 间的整数.
内计算 . 把结果表示成 0 到 间的整数.
乘幂填空
考虑映射
, 它把
映到
. 根据
的值把底下方块里的数拖放到空格里去.
同余根
设
是素数 . 我们希望算出整数
使得
 mod .
mod .
- 计算整数
使得
模
同余于 1, 请求出
, 它在后面还有用.
=
=
- 应该计算
的多少次幂 ?
- 计算一个解
=
mod .
根
是素数. 在  /
/ 内有元素 a , 使得 a 模 同余于 , 求 a.
内有元素 a , 使得 a 模 同余于 , 求 a. 把结果表示成 0 到 间的整数.
Z/pZ 内的单位根 (I)
设方程
 1 mod .
1 mod .
计算最小整数
使得这个方程等价于
 1 mod
1 mod
并给出解的个数
Z/pZ 内的单位根 (II)
设方程组
计算最小整数
使得这个方程等价于
 1 mod .
1 mod .
模 后的解数是多少 ?
模 n 的简单计算
在  /
/ 内计算 . 把结果表示成 0 到 间的整数.
内计算 . 把结果表示成 0 到 间的整数.
平方
求  /
/ 内平方元的集合. (
内平方元的集合. ( /
/ 里的平方是可表成另一个元素平方的元素.)
里的平方是可表成另一个元素平方的元素.) 把每个元素表示成 0 到 间的整数, 元素间用逗号分隔.
和与积
求两个整数 , 满足 0 
 , 0
, 0 
 ,
, +  (mod ) , ×
(mod ) , ×  (mod ) .
(mod ) .
不考虑这两个数的次序.
模 n 线性方程组 II
求出以下线性方程组在  内的所有解
内的所有解
把解写成以下形式 其中
和
在  内.
内.
模 n 线性方程组 I
设有线性方程组
是否有模 的唯一解 ?
模 n 线性方程组 III
求出以下线性方程组在  内的所有解
内的所有解
把解写成以下形式 其中
和
在  内.
内.
三项式填空
考虑映射
, 它把
映到
. 根据
的值把底下方块里的数拖放到空格里去.
由于 WIMS 不能识别您的浏览器, 本页不能正常显示.
请注意: WIMS 的网页是交互式的: 它们不是通常的 HTML 文件. 只能在线交互地
使用. 您用自动化程序收集的网页是无用的.
- Description: 环 Z/nZ 上的一组练习. This is the main site of WIMS (WWW Interactive Multipurpose Server): interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: wims, mathematics, mathematical, math, maths, interactive mathematics, interactive math, interactive maths, mathematic, online, calculator, graphing, exercise, exercice, puzzle, calculus, K-12, algebra, math閙atique, interactive, interactive mathematics, interactive mathematical, interactive math, interactive maths, mathematical education, enseignement math閙atique, mathematics teaching, teaching mathematics, algebra, geometry, calculus, function, curve, surface, graphing, virtual class, virtual classes, virtual classroom, virtual classrooms, interactive documents, interactive document, algebra, number theory, arithmetic, arithmetic, modular, modulo, congruence
 内
.
计算
mod
.
内
.
计算
mod
.  /n
/n 里的计算的练习.
里的计算的练习.
 /
/ 里计算 / . 把结果表示成 0 到 的整数.
里计算 / . 把结果表示成 0 到 的整数.
 /
/ 里计算 / . 把结果表示成 0 到 的整数.
里计算 / . 把结果表示成 0 到 的整数.
 /
/ 里计算 / . 把结果表示成 0 到 的整数.
里计算 / . 把结果表示成 0 到 的整数.
 /
/ 里的零因子吗 ?
里的零因子吗 ?
 /
/ 里的零因子集. (这个练习的零因子不包括 0.)
里的零因子集. (这个练习的零因子不包括 0.)  /
/ 里有多少零因子 ?
里有多少零因子 ?  /
/ 内有两个根
与
.
计算之.
内有两个根
与
.
计算之.  内
.
计算
mod
.
内
.
计算
mod
.  /
/ 里求 的逆 . 把结果表示成 0 到 间的整数.
里求 的逆 . 把结果表示成 0 到 间的整数.
 /
/ 里求 的逆 . 把结果表示成 0 到 的整数.
里求 的逆 . 把结果表示成 0 到 的整数.
 /
/ 里求 的逆 . 把结果表示成 0 到 的整数.
里求 的逆 . 把结果表示成 0 到 的整数.
 /
/ ->
->  /
/ 它定义为 f(x)=x .
它定义为 f(x)=x .  内方程
内方程  mod
mod  其中
是正整数,
是
其中
是正整数,
是 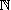 内严格小于
的整数的有限集. 取
为其中最小者, 给出
内所有整数 .
解的集合
具有形式
内严格小于
的整数的有限集. 取
为其中最小者, 给出
内所有整数 .
解的集合
具有形式
 其中
是
内严格小于 的整数的有限集. 写出
的所有整数.
其中
是
内严格小于 的整数的有限集. 写出
的所有整数.


 /
/ 内计算 . 把结果表示成 0 到 间的整数.
内计算 . 把结果表示成 0 到 间的整数.
 /
/ 内计算 . 把结果表示成 0 到 间的整数.
内计算 . 把结果表示成 0 到 间的整数.
 mod .
mod .  /
/ 内有元素 a , 使得 a 模 同余于 , 求 a.
内有元素 a , 使得 a 模 同余于 , 求 a.  1 mod .
1 mod .  1 mod
1 mod  1 mod .
1 mod . /
/ 内计算 . 把结果表示成 0 到 间的整数.
内计算 . 把结果表示成 0 到 间的整数.
 /
/ 内平方元的集合. (
内平方元的集合. ( /
/ 里的平方是可表成另一个元素平方的元素.)
里的平方是可表成另一个元素平方的元素.) 
 , 0
, 0 
 ,
,  (mod ) , ×
(mod ) , ×  (mod ) .
(mod ) .  内的所有解
内的所有解  内.
内.
 内的所有解
内的所有解  内.
内.