OEF continuity
--- Introduction ---
This module actually gathers 5 exercises on the continuity
(definition and fundamental properties) of functions of one real variable.
Continuity and sequences
Let
be a real function. Are the following statements justified? A. If , then .
B. If , then .
Epsilon - Delta
Let
be a real function such that: For all
, there exists a
such that
implies
.
What does this mean to the continuity of
?
Epsilon - Delta II
Let
be a real function such that:
,
,
such that
.
What does this mean to the continuity of
?
Mixed multiplication
Let
be a real function. Is the following statement true? If
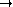
is continuous, then
is continuous.
Powers
Let
be a real function. Is the following statement true? If is continuous, then is continuous.
This page is not in its usual appearance because WIMS is unable to recognize your
web browser.
Please take note that WIMS pages are interactively generated; they are not ordinary
HTML files. They must be used interactively ONLINE. It is useless
for you to gather them through a robot program.
- Description: collection of exercises ont the continuity of functions of one real variable. This is the main site of WIMS (WWW Interactive Multipurpose Server): interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: wims, mathematics, mathematical, math, maths, interactive mathematics, interactive math, interactive maths, mathematic, online, calculator, graphing, exercise, exercice, puzzle, calculus, K-12, algebra, mathématique, interactive, interactive mathematics, interactive mathematical, interactive math, interactive maths, mathematical education, enseignement mathématique, mathematics teaching, teaching mathematics, algebra, geometry, calculus, function, curve, surface, graphing, virtual class, virtual classes, virtual classroom, virtual classrooms, interactive documents, interactive document, analysis, continuity,limit,sequence,real_function, calculus
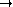 is continuous, then
is continuous.
is continuous, then
is continuous. 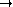 is continuous, then
is continuous.
is continuous, then
is continuous.