Trinôme du second degré

Introduction et sommaire

Nous étudions ici les trinômes du second degré à coefficients réels. Le fait que les coefficients et les racines considérées sont réels sera parfois sous-entendu.

Définition. Soient

a

non nul,

b

c

trois réels. On appelle trinôme du second degré en $x$ à coefficients réels l'expression

a x^{2} + b x + c

.
Quand elles existent, les solutions réelles de l'équation du second degré (E) :

a x^{2} + b x + c = 0

sont appelées racines réelles du trinôme.

On pose $T (x) = a x^{2} + b x + c$ . Le but de cette étude est la factorisation de ce trinôme $T (x)$ et la résolution de l'équation (E). On s'intéressera aussi au signe de $T (x)$ et à l'interprétation graphique des résultats.

Sommaire

Problème et cas particulier
Forme canonique d'un trinôme
Résolution d'une équation du second degré à coefficients réels
- Théorème
- Exemples de résolution et exercices
- Exemples de factorisation d'un trinôme
- Somme et produit des racines et techniques de vérification.
Interprétation graphique
Signe d'un trinôme
Position d'un nombre par rapport aux racines
Inéquation du second degré

Problème et cas particulier

Problème. Soient

a

non nul,

b

c

trois réels. Considérons le trinôme du second degré en

x

à coefficients réels

T (x) = a x^{2} + b x + c

et l'équation (E)

a x^{2} + b x + c = 0

. Notre but est de résoudre l'équation (E) et de factoriser ce trinôme

T (x)

Commençons par résoudre le problème posé dans le cas particulier où

b

est nul :

T (x) = a x^{2} + c

, c'est-à-dire

T (x) = a (x^{2} + \frac{c}{a})

Si $\frac{c}{a}$ est strictement positif, le trinôme est factorisé et l'équation (E) n'admet aucune solution réelle.
Si $\frac{c}{a}$ est nul, le trinôme est factorisé et l'équation (E) admet la solution réelle $0$ .
Si $\frac{c}{a}$ est strictement négatif, on factorise le trinôme en utilisant l'identité remarquable : $u^{2} - v^{2} = (u + v) (u - v)$ : $T (x) = a (x + \sqrt{- \frac{c}{a}}) (x - \sqrt{- \frac{c}{a}})$ . L'équation (E) admet deux solutions réelles $r_{1} = \sqrt{- \frac{c}{a}}$ et $r_{2} = - \sqrt{- \frac{c}{a}}$ .

Pour s'exercer :

Résolution du cas particulier
Résolution simple

Forme canonique d'un trinôme

Proposition et définition. Soient

a

non nul,

b

c

trois réels. Pour tout réel

x

, on a l'égalité :

$T (x) = a x^{2} + b x + c = a [{(x + \frac{b}{2 a})}^{2} - (\frac{b^{2} - 4 ac}{4 a^{2}})]$

On dit que $a [{(x + \frac{b}{2 a})}^{2} - (\frac{b^{2} - 4 ac}{4 a^{2}})]$ est la forme canonique de $T (x)$ .

Avec les notations suivantes :

α = - \frac{b}{2 a}

β = - \frac{b^{2} - 4 ac}{4 a}

, la forme canonique s'écrit :

T (x) = a (x - α)^{2} + β

On constate que l'on a : $β = T (α)$ . L'interprétation géométrique du couple $(α, β)$ est donnée à cette page .

Démonstration.

Comme

a

n'est pas nul, en s'inspirant de l'identité remarquable :

(x + u)^{2} = x^{2} + 2 ux + u^{2}

, on peut écrire :

$T (x) = a (x^{2} + \frac{b}{a} x + \frac{c}{a}) = a [{(x + \frac{b}{2 a})}^{2} + \frac{c}{a} - \frac{b^{2}}{4 a^{2}}] = a [{(x + \frac{b}{2 a})}^{2} - (\frac{b^{2} - 4 ac}{4 a^{2}})] = a {(x + \frac{b}{2 a})}^{2} - (\frac{b^{2} - 4 ac}{4 a})$ .

Pour s'exercer :

Forme canonique
Forme canonique

Résolution d'une équation du second degré à coefficients réels

Ce théorème présente les résultats de résolution d'une équation du second degré à coefficients réels. Il s'appuie sur la forme canonique et sa factorisation.

Théorème

Soient $a$ , $b$ et $c$ trois réels. On suppose $a$ non nul. Considérons le trinôme du second degré en $x$ à coefficients réels $T (x) = a x^{2} + b x + c$ et l'équation (E) : $a x^{2} + b x + c = 0$ . On appelle discriminant de $T (x)$ ou de (E) le réel $Δ = b^{2} - 4 a c$ .

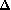Si Delta est strictement négatif, (E) n'a pas de solution réelle. La forme canonique de $T (x)$ est sa forme factorisée.

$T (x) = a [{(x + \frac{b}{2 a})}^{2} - \frac{Δ}{4 a^{2}}]$

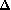Si Delta est nul, posons : $r = \frac{- b}{2 a}$ .
Le trinôme $T (x)$ se factorise ainsi : $a x^{2} + b x + c = a (x - r)^{2}$ et (E) admet $r$ comme unique solution réelle.

Si $Δ$ est strictement positif, posons : $r_{1} = \frac{- b + \sqrt{Δ}}{2 a}$ et $r_{2} = \frac{- b - \sqrt{Δ}}{2 a}$ .
Le trinôme $T (x)$ se factorise ainsi : $a x^{2} + b x + c = a (x - r_{1}) (x - r_{2})$ et (E) admet deux solutions réelles distinctes : $r_{1}$ et $r_{2}$ .

Remarque. Si $a$ et $c$ sont de signe contraires alors $Δ$ est positif.

Démonstration. Avec la notation du discriminant, la forme canonique s'écrit :

T (x) = a [{(x + \frac{b}{2 a})}^{2} - (\frac{Δ}{4 a^{2}})]

Trois cas se présentent :

Si $Δ$ est strictement négatif, l'expression $(x + \frac{b}{2 a})^{2} - \frac{Δ}{4 a^{2}}$ est strictement positive pour tout réel $x$ donc $T (x)$ ne s'annule pas et (E) n'a pas de solution. La forme canonique est la forme factorisée.
Si $Δ$ est nul, posons $r = \frac{- b}{2 a}$ . La forme canonique est la forme factorisée : $a x^{2} + b x + c = a (x - r)^{2}$ et (E) admet $r$ comme une unique solution.
Si $Δ$ est strictement positif, posons $r_{1} = \frac{- b + \sqrt{Δ}}{2 a}$ et $r_{2} = \frac{- b - \sqrt{Δ}}{2 a}$ . En utilisant l'identité remarquable : $u^{2} - v^{2} = (u + v) (u - v)$ , on obtient : $x^{2} + \frac{b}{a} x + \frac{c}{a} = (x - r_{1}) (x - r_{2})$ . On en déduit : $T (x) = a (x - r_{1}) (x - r_{2})$ . Comme un produit est nul si et seulement si l'un au moins de ses facteurs est nul, $r_{1}$ et $r_{2}$ sont les solutions de (E).

Exemples de résolution et exercices

Pour consulter le théorème

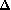Si Delta est strictement négatif, (E) n'a pas de solution réelle. La forme canonique de $T (x)$ est sa forme factorisée.

$T (x) = a [{(x + \frac{b}{2 a})}^{2} - \frac{Δ}{4 a^{2}}]$

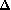Si Delta est nul, posons : $r = \frac{- b}{2 a}$ .
Le trinôme $T (x)$ se factorise ainsi : $a x^{2} + b x + c = a (x - r)^{2}$ et (E) admet $r$ comme unique solution réelle.

Exemple 1. Résoudre l'équation

= 0

.
Le discriminant vaut

1

. L'équation a deux solutions :

r_{1} = - 2

r_{2} = - 1

. La forme factorisée du trinôme est

() ()

Consultez les exemples à solution cachée :

Exemple 2
Exemple 3

Remarque. Si le trinôme est donné sous forme factorisée $a (x - u) (x - v)$ , ses racines sont évidemment $u$ et $v$ .

Exercices.

Trinôme factorisé
Résolution sans $\Delta$
Résolution d'une équation du second degré

Exemple 2

Pour consulter le théorème

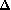Si Delta est strictement négatif, (E) n'a pas de solution réelle. La forme canonique de $T (x)$ est sa forme factorisée.

$T (x) = a [{(x + \frac{b}{2 a})}^{2} - \frac{Δ}{4 a^{2}}]$

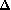Si Delta est nul, posons : $r = \frac{- b}{2 a}$ .
Le trinôme $T (x)$ se factorise ainsi : $a x^{2} + b x + c = a (x - r)^{2}$ et (E) admet $r$ comme unique solution réelle.

Résoudre l'équation $= 0$ .

Solution

Exemple 3

Pour consulter le théorème

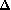Si Delta est strictement négatif, (E) n'a pas de solution réelle. La forme canonique de $T (x)$ est sa forme factorisée.

$T (x) = a [{(x + \frac{b}{2 a})}^{2} - \frac{Δ}{4 a^{2}}]$

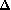Si Delta est nul, posons : $r = \frac{- b}{2 a}$ .
Le trinôme $T (x)$ se factorise ainsi : $a x^{2} + b x + c = a (x - r)^{2}$ et (E) admet $r$ comme unique solution réelle.

Résoudre l'équation .

Solution

Exemples de factorisation d'un trinôme

On rappelle le résultat de factorisation du théorème . La factorisation s'obtient aussi directement depuis la forme canonique.

r_{1}

r_{2}

sont les racines distinctes ou égales du trinôme

T (x) = a x^{2} + b x + c

, celui se factorise ainsi :

T (x) = a (x - r_{1}) (x - r_{2})

.
Si le trinôme n'a pas de racine, il ne se factorise pas.

Exemple générique. Pour factoriser le trinôme , on calcule ses racines.
Le discriminant vaut

1

.
L'équation a deux solutions :

r_{1} = 2

r_{2} = 1

.
On obtient la factorisation suivante :

=

Exemples simples. Parfois la factorisation est immédiate sans calcul du discriminant :

$3 x^{2} - x = x (3 x - 1)$
$(2 x - 1)^{2} - 25 = (2 x - 6) (2 x + 4)$
$(2 x - 1)^{2} + 25$ est factorisé au maximum.

Pour s'exercer :

Factorisation simple
Factorisation

Somme et produit des racines

Cette page n'est pas au programme des terminales mais bien utile pourtant.

Proposition. Soit

a x^{2} + b x + c

un trinôme du second degré en

x

admettant

r_{1}

r_{2}

comme racines distinctes ou égales.
Alors on a les égalités suivantes :

(r_{1} + r_{2}) = - \frac{b}{a}

(r_{1} \times r_{2}) = \frac{c}{a}

.
Les réels

r_{1}

r_{2}

sont solutions de

x^{2} - S x + P = 0

avec

S = r_{1} + r_{2}

P = r_{1} \times r_{2}

Démonstration. En développant le second membre de l'égalité :

a x^{2} + b x + c = a (x - r_{1}) (x - r_{2})

, on obtient

a x^{2} + b x + c = a [x^{2} - (r_{1} + r_{2}) x + r_{1} \times r_{2}

]. Par identification, on en déduit les égalités demandées.

Techniques de vérification.

Pour vérifier que $t$ est solution de $a x^{2} + b x + c = 0$ , on peut calculer $a t^{2} + b t + c$ et constater qu'on obtient $0$ .
Pour vérifier que $u$ et $v$ sont les deux racines de $a x^{2} + b x + c = 0$ , on calcule la somme $S = u + v$ et on vérifie qu'on obtient $S = - \frac{b}{a}$ . Si c'est le cas, on calcule $P = u v$ et on vérifie qu'on obtient $P = \frac{c}{a}$ .
On remarque que les deux racines sont de même signe si et seulement si $P = \frac{c}{a}$ est positif.

Exemple 1. Résoudre l'équation

= 0

.
Le discriminant vaut

1

.
L'équation a deux solutions :

r_{1} = 3

r_{2} = 4

.
On a bien :

\frac{b}{a} = - 7 = - (r_{1} + r_{2})

\frac{c}{a} = 12 = r_{1} \times r_{2}

Exemple 2. Un champ rectangulaire a un périmètre de $1 800 m$ et une superficie de $200 000 m^{2}$ . Quelles sont ses dimensions ?
Ses dimensions $L$ et $ℓ$ vérifient les égalités suivantes : $L + ℓ = 900$ et $L ℓ = 200 000$ . Elles sont donc solution de l'équation : $x^{2} - 900 x + 200 000 = 0$ dont les solutions sont $L = 500$ et $ℓ = 400$ .

Pour s'exercer :

Calculer la somme et le produit des racines sans les calculer.
Calculer la somme et le produit des racines sans les calculer.
Trouver deux nombres connaissant leur somme et leur produit
Calculer la valeur de résistances

Interprétation graphique

Nous allons donner une interprétation graphique de la forme canonique et du théorème .

En considérant le trinôme sous sa forme canonique $a x^{2} + b x + c = a [{(x + \frac{b}{2 a})}^{2} - \frac{Δ}{4 a^{2}}]$ , on voit que la valeur minimale (si $a$ est positif) ou maximale (si $a$ est négatif) de $y$ est obtenue en $α = - \frac{b}{2 a}$ .

Soit une parabole d'équation

y = a x^{2} + b x + c

. Posons

Δ = b^{2} - 4 a c

. Le sommet de la parabole a pour coordonnées

(- \frac{b}{2 a}, - \frac{Δ}{4 a})

.
Les racines du trinôme sont les abscisses des points d'intersection (s'ils existent) de la parabole et de l'axe des abscisses.

Le graphique présente la parabole d'équation $y =$ . Dans cet exemple, le coefficient $a$ est positif et 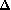Delta est égal à $25$ .
Comme le discriminant est positif, le sommet (point vert) de la parabole, de coordonnées $(0.75, - 3.125)$ , est sous la droite $y = 0$ . Les solutions de l'équation $= 0$ , $r_{1} =$ et $r_{2} =$ , sont les abscisses des points d'intersection (en rouge) de la parabole et de la droite $y = 0$ .

Le cas $a$ négatif est symétrique par rapport à l'axe des $x$ . Dans ce cas, la parabole est orientée vers le bas. Ce cas est traité dans les figures illustrant l' étude du signe du trinôme .

Pour s'exercer :

Orientation d'une parabole
Allure d'une parabole
Correspondance Parabole - Trinôme
Sommet d'une parabole
Nombre de points d'intersection avec l'axe des $x$
Reconnaître l'équation d'une parabole

Signe d'un trinôme

La forme factorisée du trinôme nous permet d'en étudier le signe. Nous présentons dans un tableau le signe de $a x^{2} + b x + c$ selon la valeur de $x$ .

Si le trinôme $a x^{2} + b x + c$ n'a pas de racine ou une racine double, on a vu dans la démonstration du théorème de résolution qu'il a même signe que le coefficient $a$ de $x^{2}$ . Dans le cas où le discriminant est nul, on note $r$ la racine double $\frac{- b}{2 a}$ .
Si le trinôme $a x^{2} + b x + c$ a deux racines distinctes, son signe dépend du signe de $a$ et de celui de chacun de ses facteurs, donc de la position de $x$ par rapport aux racines. Dans ce cas, on appelle $r'$ la plus petite des racines et $r ″$ l'autre racine. Les facteurs $(x - r')$ et $(x - r ″)$ sont de signes contraires si et seulement si $x$ appartient à $[r', r ″]$ . Le trinôme est du signe de $a$ à l'extérieur des racines, du signe de $- a$ entre les racines.

$Δ < 0$	$x$	$ℝ$
	$a x^{2} + b x + c$	signe de $a$
$Δ = 0$	$x$				$r$
	$a x^{2} + b x + c$	signe de $a$			0	signe de $a$
$Δ > 0$	$x$		$r'$				$r ″$
	$a x^{2} + b x + c$	signe de $a$	0	signe de $- a$			0	signe de $a$

Figure. Voir le signe du trinôme sur un graphique

Pour s'exercer :

Signe d'un trinôme avec un tableau
Tableau de signe à construire
Résolution d'inéquation à l'aide d'un tableau à construire

Illustration graphique pour l'étude du signe du trinôme

Voici un graphique pour illustrer l'étude du signe du trinôme. Les racines du trinôme sont les abscisses des points d'intersection (rouges s'ils existent) de la parabole et de l'axe des abscisses. L'ensemble des $x$ pour lesquels le trinôme est positif (sur la représentation graphique) est dessiné en vert.

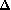Ce graphique présente la parabole d'équation $y =$ . Dans cet exemple, $a = - 2$ est négatif et Delta est égal à $17$ .
Comme le discriminant est positif, le trinôme change de signe aux points $r_{1} =$ et $r_{2} =$ , solutions de l'équation $= 0$ . Il est positif entre ses deux racines.

Position d'un nombre par rapport aux racines

Cette page n'est pas au programme des terminales. C'est une application presque directe des page précédentes.

Problème. Soient $a$ , $b$ et $c$ trois réels. On suppose $a$ non nul. Considérons le trinôme du second degré en $x$ à coefficients réels $T (x) = a x^{2} + b x + c$ admettant deux racines $r_{1}$ et $r_{2}$ . On suppose $r_{1} < r_{2}$ .
Soit un réel $u$ . Nous cherchons à déterminer la position de $u$ par rapport à $r_{1}$ et $r_{2}$ sans les calculer.

Etude. D'après l' étude du signe du trinôme , on peut affirmer que $u$ est entre $r_{1}$ et $r_{2}$ si et seulement si la quantité $a T (u)$ est négative.

Quand $a T (u)$ est positive, il reste à préciser de quel côté des racines se trouve $u$ . Notons $S = - \frac{b}{a}$ la somme des racines comme ici . Le nombre $\frac{S}{2}$ est le milieu de l'intervalle $] r_{1}, r_{2} [$ . Si la quantité $\frac{S}{2} - u$ est positive, alors $u$ est inférieur aux racines, sinon $u$ est supérieur aux racines.

Pour s'exercer :

En utilisant les résultats ci-dessus, on peut répondre aux questions de l'exercice Racines contenues dans un intervalle sans calculer les racines du trinôme.

Inéquation du second degré

Problème : Soit $U (x)$ et $V (x)$ deux trinômes du second degré. On veut résoudre l'inéquation $U (x) > V (x)$ . On note $𝒮$ son ensemble de solutions.

Méthode : On pose $T (x) = U (x) - V (x)$ . L'inéquation $U (x) > V (x)$ est équivalente à l'inéquation $T (x) > 0$ . L'ensemble $𝒮$ est donc l'ensemble des $x$ pour lesquels $T (x)$ est strictement positif. Pour déterminer $𝒮$ , il suffit donc d'étudier son signe $T (x)$ .

Exemple : Résolvons l'inéquation

3 x^{2} - 3 x - 5 > 2 x^{2} - 4 x + 1

Cette inéquation est équivalente à $x^{2} + x - 6 > 0$ .
Le trinôme $x^{2} + x - 6$ admet $2$ et $- 3$ comme racines et le coefficient de $x^{2}$ est positif.
Le trinôme est positif à l'extérieur des racines (voir Signe d'un trinôme )
L'ensemble des solutions de $3 x^{2} - 3 x - 5 > 2 x^{2} - 4 x + 1$ est $] - ∞, - 3 [\cup] 2, + ∞ [$ .

Pour s'exercer :

Résolution d'inéquations
Résolution d'inéquation 1
Résolution d'inéquation 2

résumé sur la méthode de résolution, l'interprétation graphique, l'étude de signe.
: equations,inequations,roots,trinomial,polynomials, wims, mathematics, mathematical, math, maths, interactive mathematics, interactive math, interactive maths, mathematic, online, calculator, graphing, exercise, exercice, puzzle, calculus, K-12, algebra, mathématique, interactive, interactive mathematics, interactive mathematical, interactive math, interactive maths, mathematical education, enseignement mathématique, mathematics teaching, teaching mathematics, algebra, geometry, calculus, function, curve, surface, graphing, virtual class, virtual classes, virtual classroom, virtual classrooms, interactive documents, interactive document

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.