OEF diagonalizacija
--- Uvod ---
Ta modul vsebuje 21 vaj o diagonalizaciji endomorfizmov
oziroma kvadratnih matrik.
Iskanje lastnih vektorjev (III)
Dani sta matriki
in
, kjer matrika
pripada nekemu endomorfizmu
v urejeni bazi
, matrika
pa je obrnljiva. Čim hitreje poiščite kakšen lastni vektor endomorfizma
, ki mu v urejeni bazi
pripada matrika
. Očitni lastni vektor za
Iskanje lastnih vektorjev (IV)
Dani sta matriki
in
, kjer matrika
pripada nekemu endomorfizmu
v urejeni bazi
, matrika
pa je obrnljiva. Čim hitreje poiščite kakšen lastni vektor endomorfizma
, ki mu v urejeni bazi
pripada matrika
. Očitni lastni vektor za
Diagonalizabilnost 2x2 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizabilnost 3x3 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizabilnost 4x4 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizabilnost 5x5 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizabilnost 6x6 (dane LVr)
Dana je matrika
. Določite razsežnosti njenih lastnih podprostorov, ki ustrezajo posameznim lastnim vrednostim: | Valeur propre | dimension des espaces propres |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ali je matrika
diagonalizabilna?
Diagonalizacija nad R (I)
Oglejte si kompleksno matriko
in ugotovite, ali je diagonalizabilna nad poljem 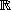 . Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
. Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
Diagonalizacija nad R (II)
Oglejte si kompleksno matriko
in ugotovite, ali je diagonalizabilna nad poljem 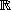 . Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
. Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
Iskanje lastnih vektorjev (I)
Naj bo V vektorski prostor razsežnosti in
njegov endomorfizem, ki mu v urejeni bazi
prostora V pripada matrika
. Brez računanja poiščite kakšen lastni vektor in ustrezno lastno vrednost endomorfizma.
Očitni lastni vektor: v =
Ustrezna lastna vrednost: 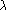 =
=
Iskanje lastnih vektorjev (II)
Naj bo V vektorski prostor razsežnosti in
njegov endomorfizem, ki mu v urejeni bazi
prostora V pripada matrika
. Brez računanja poiščite kakšen lastni vektor in ustrezno lastno vrednost endomorfizma.
Očitni lastni vektor: v =
Ustrezna lastna vrednost: 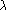 =
=
Matrike reda 2
Realna matrika
je podobna matriki oblike
(v zadnjem primeru je koeficient
neničeln).
Diagonalizabilnost 2x2 (dani LVek)
Naslednji stolpci predstavljajo lastne vektorje neke matrike A reda : Potem velja:
Diagonalizabilnost 3x3 (dani LVek)
Naslednji stolpci predstavljajo lastne vektorje neke matrike A reda : Potem velja:
Diagonalizabilnost 4x4 (dani LVek)
Naslednji stolpci predstavljajo lastne vektorje neke matrike A reda : Potem velja:
Diagonalizabilnost 5x5 (dani LVek)
Naslednji stolpci predstavljajo lastne vektorje neke matrike A reda : Potem velja:
Lastne vrednosti 1
Naj bo
končnorazsežen vektorski prostor nad poljem
in
njegov endomorfizem. Kaj lahko poveste o pravilnosti naslednje trditve:
Če je endomorfizem
, potem .
Lastne vrednosti 2
Naj bo
vektorski prostor razsežnosti nad poljem
in
njegov endomorfizem. Ali ima
vedno najmanj eno lastno vrednost iz polja
?
Lastne vrednosti 3
Naj bo
vektorski prostor nad poljem
in
njegov endomorfizem. Naj bo
in 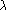 , tako da je
. Ali smemo sklepati, da je
, tako da je
. Ali smemo sklepati, da je 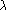 lastna vrednost endomorfizma
?
lastna vrednost endomorfizma
?
Slika in lastni vektorji 1
| Endomorfizem
prostora
ima lastna vektorja
() pri lastni vrednosti in
() pri lastni vrednosti . Določite sliko vektorja
glede na ta endomorfizem. S klikom označite krajišče iskanega vektorja. |
|
Slika in lastni vektorji 2
| Endomorfizem
prostora
ima lastna vektorja
() pri lastni vrednosti in
() pri lastni vrednosti . Določite sliko vektorja
glede na ta endomorfizem. S klikom označite krajišče iskanega vektorja. |
|
- Description: zbirka vaj iz diagonalizacije matrik. This is the main site of WIMS (WWW Interactive Multipurpose Server): interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: wims, mathematics, mathematical, math, maths, interactive mathematics, interactive math, interactive maths, mathematic, online, calculator, graphing, exercise, exercice, puzzle, calculus, K-12, algebra, mathématique, interactive, interactive mathematics, interactive mathematical, interactive math, interactive maths, mathematical education, enseignement mathématique, mathematics teaching, teaching mathematics, algebra, geometry, calculus, function, curve, surface, graphing, virtual class, virtual classes, virtual classroom, virtual classrooms, interactive documents, interactive document, linear algebra, diagonalizacija, lastna vrednost, lastni vektor
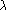 =
=
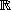 . Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
. Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
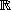 . Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
. Vnesite tudi razsežnost vsote njenih lastnih podprostorov.
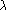 =
=
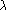 =
=
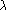 , tako da je
. Ali smemo sklepati, da je
, tako da je
. Ali smemo sklepati, da je 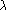 lastna vrednost endomorfizma
?
lastna vrednost endomorfizma
?