OEF Sommations finies --- Introduction ---

Ce module regroupe pour l'instant 11 exercices sur la manipulation des sommes et produits.

Changement de variable dans une somme 1

On désigne par une fonction définie sur les entiers et on pose :
.
Transformez l'expression de en faisant le changement de variable
Bonne réponse
Expression incorrecte Dans la première expression de , les valeurs écrites en-dessous et au-dessus de la somme indiquent que l'on somme les valeurs de en faisant prendre à successivement chaque entier de à , il faut que votre expression ait la même propriété.
Avec ces indications, corrigez votre première expression :

Changement de variable dans une somme 2

On pose :
.
Transformez l'expression de en faisant le changement de variable
Bonne réponse
Expression incorrecte
  • les bornes de la somme ne peuvent pas dépendre de la valeur du paramètre .
  • les bornes de la somme ne peuvent pas dépendre de la valeur du paramètre .
  • le terme général de votre somme n'est pas correct.
  • la valeur écrite en-dessous du signe somme indique la plus petite valeur que va prendre la variable et la valeur écrite au-dessus du signe somme indique sa plus grande valeur.
  • votre expression ne contient pas le bon nombre de termes.
Dans la première expression de , les valeurs écrites en-dessous et au-dessus de la somme indiquent que l'on somme les valeurs de en faisant prendre à successivement chaque entier de à , il faut que votre expression ait la même propriété.
Avec ces indications, corrigez votre première expression :

Indices et sommation

On désigne par une fonction définie sur les entiers et on pose : .
Donner une autre expression de en faisant une translation sur la variable :
Expression incorrecte,

Interversion de sommes

Soit une famille de réels. On pose .
Lorsqu'on intervertit les deux sommes, on obtient :
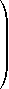left4 right4
=
Consigne : la borne d'en bas doit être inférieure à celle d'en haut. On pourra utiliser les fonctions min et maxsous la forme max(i,2) par exemple. Mais les formules devront être simplifiées : on n'écrira pas max(6,13) à la place de 13 par exemple !

Sommation 1

Voici un ensemble d'entiers :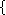

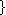
leftbrace1 rightbrace1

On peut écrire de ses éléments sous la forme ayant le même nombre de termes, en trouver l'expression :

Sommation 2

On note l'expression suivante
+
Écrire sous la forme d'une somme unique :

Sommation double 1

On considère l'ensemble des couples tels que
et .
Écrire la somme des nombres pour sous la forme d'une somme double :

Sommation double 2

On considère l'ensemble des couples tels que et avec la condition : .
On note la somme des nombres pour .
Écrire sous la forme d'une somme double :
Consigne : la borne d'en bas doit être inférieure à celle d'en haut. On pourra utiliser les fonctions min et max sous la forme max(i,2) par exemple. Mais les formules devront être simplifiées : par exemple, on n'écrira pas max(6,13) à la place de 13.

Sommation graphique

On considère la somme double suivante sur un ensemble fini
On considère l'ensemble des couples tels que et et tels que
.
Sur l'un des dessins, l'ensemble des points rouges représente l'ensemble des éléments de . Cliquez sur ce dessin :

Somme classique 1

.
  1. .
    =
    , , .
  2. .
    , , .
  3. . :
    .

Somme classique 2

.
  1. .
    =
    , , .
  2. .
    , , .
  3. . :
    , .
Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.