OEF 熵
--- 介绍 ---
本模块目前包含 19 个关于信息论的熵的练习.
小数-3
计算以下 3 个概率分布:
{ , , } 的二进熵(比特).
小数-4
计算以下 4 个概率分布:
{ , , , } 的二进熵(比特).
小数-5
计算以下 5 个概率分布:
{ , , , , } 的二进熵(比特).
已知熵 - 2
请找出 2 元系统 {A,B} 的概率分布, 使得系统的二进熵(比特)等于 . 概率 P(A), P(B) 必须是正数, 而且加起来等于 1.
已知熵 - 3
请找出 3 元系统 {A,B,C} 的概率分布, 使得系统的二进熵(比特)等于 . 概率 P(A), P(B), P(C) 必须是正数, 而且加起来等于 1.
已知熵 - 4
请找出 4 元系统 {A,B,C,D} 的概率分布, 使得系统的二进熵(比特)等于 . 概率 P(A), P(B), P(C), P(D) 必须是正数, 而且加起来等于 1.
熵的存在性 - 3
是否存在 3 元系统它的二进熵(比特)等于 ?
熵的存在性
是否存在 元系统它的二进熵(比特)等于 ?
计算机文件
一个计算机文件有 个字节. 文件的每个字节只有 4 个值, 如下表所示. 分别按照文件的二进位(比特)数与字节数计算文件的二进熵(比特).
计算机文件 II
一个计算机文件有 个字节. 文件的每个字节只有 6 个值, 如下表所示. 根据字节数, 文件的二进熵(比特)为
.
通过使用最佳变长二进码对字节重新编码, 可以把文件长度缩短为
字节 (不计可能有的头部).
彩色图像
一个 × 个像素的彩色图像由黑、白、红、绿、蓝 5 种色彩构成. 每种色彩在图像里的像素数如下: 请按照像素计算图像的二进熵(比特).
熵的极大值 - 3
有一个 3 元 {A,B,C} 的概率分布系统. 已知概率 P(A) = , 问系统的二进熵(比特)的极大、极小值分别是多少?
熵的极大值 II - 3
有一个 3 元 {A,B,C} 的概率分布系统. 已知概率 P() = 并且 P(A) 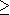 P(B)
P(B) 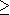 P(C) ,
P(C) , 问系统的二进熵(比特)的极大、极小值分别是多少?
分数-3
计算以下 3 个概率分布:
{ } 的二进熵(比特).
分数-4
计算以下 4 个概率分布:
{ } 的二进熵(比特).
分数-5
计算以下 5 个概率分布:
{ } 的二进熵(比特).
分数-6
计算以下 6 个概率分布:
{ } 的二进熵(比特).
条件存在性 - 3
是否存在 3 个元素 {A,B,C} 的系统, 使得 P(A) = , 而且二进熵(比特)等于 ?
条件存在性 - 4
是否存在 4 个元素 {A,B,C,D} 的系统, 使得 P(A) = , P(B) = , 而且二进熵(比特)等于 ?
由于 WIMS 不能识别您的浏览器, 本页不能正常显示.
请注意: WIMS 的网页是交互式的: 它们不是通常的 HTML 文件. 只能在线交互地
使用. 您用自动化程序收集的网页是无用的.
- Description: 一组关于熵的练习. This is the main site of WIMS (WWW Interactive Multipurpose Server): interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: wims, mathematics, mathematical, math, maths, interactive mathematics, interactive math, interactive maths, mathematic, online, calculator, graphing, exercise, exercice, puzzle, calculus, K-12, algebra, math閙atique, interactive, interactive mathematics, interactive mathematical, interactive math, interactive maths, mathematical education, enseignement math閙atique, mathematics teaching, teaching mathematics, algebra, geometry, calculus, function, curve, surface, graphing, virtual class, virtual classes, virtual classroom, virtual classrooms, interactive documents, interactive document, information theory, probability, Shanon, code
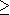 P(B)
P(B) 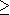 P(C) ,
P(C) , 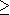 P(B)
P(B) 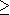 P(C) ,
P(C) ,